10th Class Geometry(ଜ୍ୟାମିତି) - Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ Ex 1(a) All Question With Answer
↓ Question & Answer ↓
(a) ନିମ୍ନ ଚିତ୍ର (a) ରେ L_1 || L_2 || L_3 ଏବଂ T_1 ଓ T_2 ଛେଦକ|
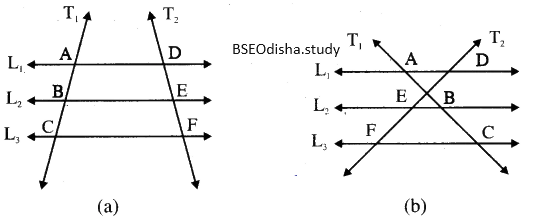
(a)(i) AB = 2 ସେ.ମି., BC = 3 ସେ.ମି. ଓ DE = 3 ସେ.ମି. ହେଲେ EF = ……….|
Solution:
(i) L_1 \parallel L_2 \parallel L_3 \Rightarrow \frac{AB}{BC} = \frac{DE}{EF}
\Rightarrow \frac{2}{3} = \frac{3}{EF} \Rightarrow EF = \frac{3 \times 3}{2}
\ = 4.5\ \text{cm}
(ii)L_1 || L_2 || L_3 ଏବଂ T_1 ଓ T_2 ଦୁଇଟି ଛେଦକ |
DE = 6 ସେ.ମି., EF = 8 ସେ.ମି. ଓ BC = 6 ସେ.ମି. 6ହ6ଲ AC = ……….|
Solution:
\therefore \frac{DE}{EF} = \frac{AB}{BC} \Rightarrow \frac{6}{8} = \frac{AB}{6}
\Rightarrow AB = \frac{6 \times 6}{8} = 4.5\ \text{ସେ.ମି.}
AC = AB + BC = 4.5\ \text{ସେ.ମି.} + 6\ \text{ସେ.ମି.} = 10.5\ \text{ସେ.ମି.}
(b)
Solution:
(i) ଏଠାରେ L_1 \parallel L_2 \parallel L_3 ଏବଂ T_1 ଓ T_2 ଦୁଇଟି ଛେଦକ
\frac{AB}{BC} = \frac{DE}{EF} \Rightarrow \frac{3}{2} = \frac{DE+EF}{EF}
\Rightarrow \frac{3+2}{2} = \frac{DE}{EF} \Rightarrow \frac{5}{2} = \frac{EF}{DF} \Rightarrow \frac{2}{5}
(ii) \overline{AC} ର ମଧ୍ୟ ବିନ୍ଦୁ B ଅଟେ, ଅର୍ଥାତ AB = BC \frac{EF}{FD} = \frac{BC}{AC} = \frac{BC}{AB+BC} = \frac{BC}{2BC} = \frac{1}{2} \Rightarrow 2EF = FD ଅତଏବ EF ହେଉଛି FD ର ଅର୍ଦ୍ଧ |
ଚିତ୍ର6ର L_1 || L_2 || L_3 ଏବଂ T_1 ଓ T_2 ଦୁଇଟି ଛେଦକ | L_2 ଓ L_3 ଉପରେ ଯଥାକ୍ରମେ G ଓ H ବିନ୍ଦୁ ଚିହ୍ନିତ ଯେପରି BG = AD ଏବଂ CH = BE;
ପ୍ରମାଣ କର 6ଯ
(i) DG : EH = DE : EF
(ii) (DG + EH) : EH = DF : EF
Solution:
ଦତ୍ତ: L_1 || L_2 || L_3 ଏବଂ T_1 ଓ T_2 ଦୁଇଟି ଛେଦକ ଯଥାକ୍ରମେL_1, L_2 ଓ L_3 କୁ A,B,C ଓ D,E,F ଦିନ୍ଦୁ6ର 6ଚ୍ଛଦକ6ର | L_2 ଉପ6ର G ଏକ ବିନ୍ଦୁ ଯେପରିBG = AD ଏର୍ବ L_3 ରପ6ର H ଏକ ଦିନ୍ଦୁ ଯେପରି CH = BE |
ପ୍ରାମାଣ୍ୟ :
(i) DG : EH = DE : EF
(ii) (DG + EH) : EH = DF : EF
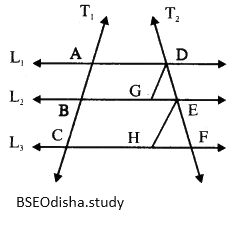 ଅଙ୍କନ: \overline{DG} ଓ \overline{EH} ଅଙ୍କନ କରାଯାଉ | |
ଅଙ୍କନ: \overline{DG} ଓ \overline{EH} ଅଙ୍କନ କରାଯାଉ | |
ପ୍ରମାଣ: (i) AD = BG (ଦତ୍ତ) (\overline{AD}∥\overline{BG}),
∵ L_1 || L_2(ଦତ୍ତ)
⇒ ABGD ଏକ ସାମାନ୍ତରିକଚିତ୍ର | AB = DG
ସେହିପରିBEHC ସାମାନ୍ତରିକଚିତ୍ର ଓ BC = EH
∴ \frac{DG}{EH} =\frac{ AB}{BC} …(1)
ପୁନଶ୍ଚ \frac{AB}{BC} =\frac{DE}{EF}
⇒ \frac{DG}{EH} = \frac{DE}{EF} (1ରୁ) (ପ୍ରମାଣିତ)
(ii) ପୂର୍ବରୁ ପ୍ରମାଣିତ\frac{DG}{EH} = \frac{DE}{EF}
⇒ \frac{DG+EH}{EH} = \frac{DE+EF}{EF}
⇒ \frac{DG+EH}{EH} = \frac{DE}{EF} (ପ୍ରମାଣିତ)
Question 3.
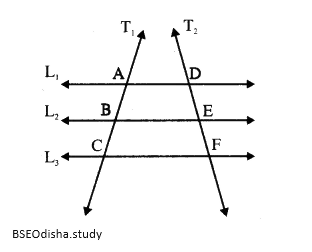
ନିମ୍ନ ଚିତ୍ରରେ L1 || L2 || L3 ଏବଂ T1, ଓ T2, ଦୁଇଟି ଛେଦକ । ଯଦି AB = BC ହୁଏ, ପ୍ରମାଣ କର ଯେ 2 BE = AD + CF |
ଦତ୍ତ : L1 || L2 || L3 ଛେଦକ T1 ଓ T2 , L1, L2, ଓ L3, କୁ ଯଥାକ୍ରମେ A, B, C ଓ D, E, F ବିନ୍ଦୁରେ ଛେଦ କରେ ଏବଂ AB = BC |
ପ୍ରାମାଣ୍ୟ : 2BE = AD + CF
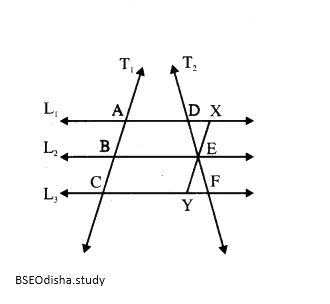
ଅକନ : E ଦିଦୁ ମଧ୍ୟ6ଦଇ \overline{AC} ସହ ସାମନ୍ତର ଭାବେ ଅଙ୍କିତ ରେଖା L1 || L3 କୁ ଯଥାକ୍ରମେ X ଓ Y ବିନ୍ଦୁରେ ଛେଦକରୁ |
ପ୍ରମାଣ : \overline{AX }∥\overline{BE} ଓ \overline{AB}∥\overline{EX} ⇒ABEX ସାମନ୍ତରିକ ଚିତ୍ର |
⇒ AX = BE ଓ AB = EX
ସେହିପରି BCYE ଏକ ସାମନ୍ତରିକ ଚିତ୍ର |
⇒BE =CY ଓ BC = EY
 AB = BC (ଦତ୍ତ ) ⇒ EX = EY,
AB = BC (ଦତ୍ତ ) ⇒ EX = EY,\triangle{EDX} ଓ \triangle{EYF}
\because \begin{cases} \angle{DXE} \cong \angle{EYF} (ଏକାନ୍ତର କୋଣ)\\ \angle{XED} \cong \angle{YEF} (ପ୍ରତୀପ କୋଣ)\\ EX=EY \end{cases}
\Rightarrow \Delta {EDX} \cong \Delta {EYF} (କୋ - ବା - କୋ ସର୍ବସମତା )
\Rightarrow {DX} = {YF}
\therefore {ଦକ୍ଷିଣପକ୍ଷ} = {AD} + {CF}={AX}-{DX}+{CY}+{YF}
= {BE} - {DX}+{BE}+{DX}(\because {YF}={DX})
= 2BE = ବାମପକ୍ଷ